Outstanding Tips About How To Do Node Voltage Analysis

Lesson 1 Intro To Node Voltage Method (Engineering Circuits) Math
Unlocking Circuit Secrets
1. What's the Buzz About Node Voltage?
Ever stared at a circuit diagram, feeling like you're looking at a tangled mess of wires? Don't worry, you're not alone! Node voltage analysis (sometimes called nodal analysis) is a powerful technique that helps us unravel those circuits and figure out what's going on with the voltages at different points. Think of it like finding the altitude at different spots on a mountain range — it helps you understand the lay of the land, or in this case, the electrical landscape.
Essentially, node voltage analysis uses Kirchhoff's Current Law (KCL) and Ohm's Law to set up equations that describe the current flow at each "node" in the circuit. A node is simply a point where two or more circuit elements connect. By solving these equations, we can determine the voltage at each node, which then allows us to calculate currents and power throughout the circuit. It might sound intimidating, but with a little practice, it becomes surprisingly intuitive.
So, why bother learning this? Well, node voltage analysis is incredibly versatile. It works well for circuits with multiple voltage or current sources, and it's a fundamental tool for circuit designers and electrical engineers. It is like being able to see the matrix, you can analyze and design circuit with ease.
I remember when I first learned about node voltage analysis. I was totally lost! My professor just kept saying "KCL this, Ohm's Law that" and I thought, "Where are the actual instructions??" Luckily, I found a good resource (not this article, because it didn't exist yet!), and now I'm hoping to pay it forward and make things a little clearer for you. So, let's dive in!

Step-by-Step
2. Identify the Nodes
First things first, you need to identify all the nodes in your circuit. Remember, a node is a point where two or more circuit elements connect. It's like finding the intersections on a map. Usually, the most negative voltage point in the circuit is taken as ground, with voltage 0. All other voltage will be measured with ground as reference.
Often, one of the nodes is designated as the "reference node" or "ground." This node is assigned a voltage of 0 volts, and all other node voltages are measured relative to it. Choosing a node with many connections as your ground can often simplify your calculations later. A good ground node is one that shares the most elements.
Keep in mind that a wire itself constitutes a node; all points along a single, continuous wire have the same voltage. Don't overthink it; just look for where components join together. Its like finding where all the roads converge.
Don't be afraid to redraw the circuit if it helps you visualize the nodes more clearly. Sometimes, a simple rearrangement can make the whole process much easier. Think of it like reorganizing your desk before tackling a big project; it can make a surprising difference.
3. Apply Kirchhoff's Current Law (KCL)
KCL states that the sum of currents entering a node is equal to the sum of currents leaving the node. In other words, what goes in must come out. This is based on the principle of conservation of charge, which sounds complicated but is actually pretty straightforward.
For each node (except the reference node), write a KCL equation. Express each current in terms of the node voltages and the resistances of the connected elements using Ohm's Law (V = IR, rearranged as I = V/R). Remember, current flows from higher potential to lower potential. For each branch going out from your node, determine it's voltage difference over resistance.
For example, if you have a resistor connected between node 'a' (with voltage Va) and node 'b' (with voltage Vb), the current flowing from node 'a' to node 'b' is (Va - Vb) / R, where R is the resistance of the resistor. Careful about the directions of current!
This can sometimes feel a bit like solving a puzzle, figuring out which voltages to subtract and which resistances to divide by. But remember the basic principle of current flow, and you'll get the hang of it. It's like learning to ride a bike; wobbly at first, but eventually, it clicks.
4. Solve the System of Equations
Now you have a system of equations (one for each non-reference node) with the node voltages as unknowns. There are several methods you can use to solve these equations, including substitution, Gaussian elimination, or using a matrix solver (if the system is complex).
Substitution involves solving one equation for one variable and then substituting that expression into the other equations. This process is repeated until you have a single equation with a single unknown, which you can then solve directly. This method is great for smaller circuits.
Gaussian elimination is a more systematic approach that involves manipulating the equations to eliminate variables one by one. It's particularly useful for larger circuits with more complex systems of equations. You can use online tools to help you through the Gaussian Elimination process.
Don't be afraid to use a calculator or computer software to solve the equations, especially for larger circuits. The important thing is to understand the underlying principles of node voltage analysis. I once spent hours trying to solve a system of equations by hand, only to find out I had made a tiny arithmetic error in the beginning. Save yourself the headache and embrace technology!

Dealing with Voltage and Current Sources
5. Independent Voltage Sources
If a voltage source is directly connected between two nodes, it simplifies things significantly. The voltage difference between those two nodes is simply the voltage of the source. This gives you one of your node voltages right away!
For example, if a 5V voltage source is connected between node 'a' and the reference node, then Va = 5V. No need to write a KCL equation for that node! This is like getting a free piece of information; always take advantage of it.
If the voltage source is between two non-reference nodes, you have a supernode. Treat all of the elements inside the supernode as a single node. Write a KCL equation that encompasses the entire supernode. Also, remember the voltage source is giving you an equation relating the two node voltage on each side of the voltage source.
Be mindful of the polarity of the voltage source. If the positive terminal is connected to node 'a' and the negative terminal to node 'b', then Va - Vb = Vsource. If the polarity is reversed, then Vb - Va = Vsource. Getting the polarity wrong is a common mistake, so double-check before you proceed.
6. Independent Current Sources
Current sources are actually quite straightforward. If a current source is connected directly to a node, you simply include its current value in the KCL equation for that node.
If the current source is providing current into the node, you add its value to the incoming current terms in the KCL equation. If it's providing current out of the node, you add its value to the outgoing current terms.
For example, if a 2A current source is injecting current into node 'a', you would add 2A to the sum of incoming currents in the KCL equation for node 'a'. It's like adding a known ingredient to your recipe.
Current sources can sometimes make the KCL equations simpler to write, as you don't need to use Ohm's Law to express their current. They provide a direct current value, which is always welcome. Just be sure to pay attention to the direction of the current flow.
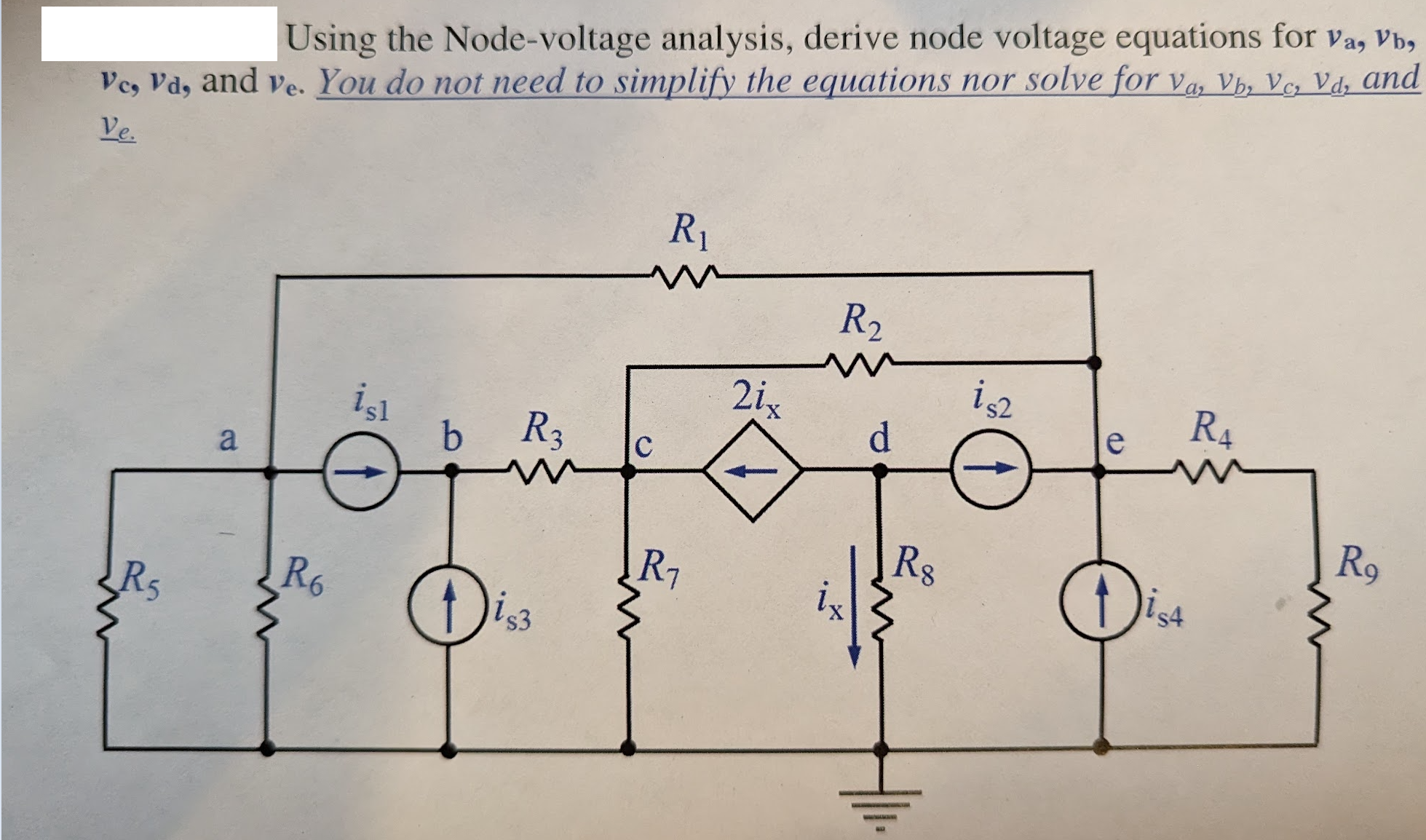
Solved Using The Nodevoltage Analysis, Derive Node Voltage
Example Time
7. A Simple Circuit
Let's consider a circuit with two resistors (R1 and R2) connected in series with a voltage source (V). The voltage source is connected to node 'a', R1 is between node 'a' and node 'b', and R2 is between node 'b' and ground.
First, we identify the nodes: node 'a', node 'b', and ground. We know that Va = V (the voltage source value). We need to find Vb.
Next, we write the KCL equation for node 'b': (Va - Vb) / R1 = Vb / R2. Notice that since R1 and R2 are connected between Va and ground, the current through R1 must be equal to the current through R2.
Now, we solve for Vb: Vb = Va * R2 / (R1 + R2). This is the voltage divider formula! Node voltage analysis allows you to derive well known theorems. See, you're already a pro!
8. A Slightly More Complex Example
Now, imagine a circuit with a voltage source (V), two resistors (R1 and R2), and a current source (I). The voltage source is connected to node 'a', R1 is between node 'a' and node 'b', R2 is between node 'b' and ground, and the current source injects current into node 'b'.
Again, we identify the nodes: node 'a', node 'b', and ground. We know that Va = V. We need to find Vb.
Now, we write the KCL equation for node 'b': (Va - Vb) / R1 + I = Vb / R2. The current from node 'a' goes into node 'b', so it is positive. There is also current directly injected from the current source into node 'b', which is also positive.
Solving the KCL equation gives us : Vb = (Va/R1 + I) / (1/R1 + 1/R2). If we plug in values we get that with Va = 10V, I = 1A, R1 = 10 ohms, and R2 = 5 ohms, we find Vb = 5V.
FAQ
9. Q
A: Dependent sources (also known as controlled sources) are voltage or current sources whose value depends on a voltage or current elsewhere in the circuit. When dealing with dependent sources, you need to express their value in terms of the node voltages. This might involve using Ohm's Law or other circuit relationships to relate the controlling voltage or current to the node voltages.
10. Q
A: Ideally choose the node to which the largest number of circuit element is connected to ground. Sometimes you have no choice about what your reference node is. Don't overthink it too much; just pick one and go with it. If you find the equations are getting too complicated, you can always switch to a different reference node. Like reorganizing a jigsaw puzzle.
11. Q
A: Yes! You'll need to use impedances (complex resistances) instead of resistances, and the voltages and currents will be phasors (complex numbers representing sinusoidal waveforms). The same principles of KCL and Ohm's Law still apply, but you'll be working with complex numbers.
